It is now increasingly common for experimental psychologists (among others) to use multilevel models (also known as linear mixed models) to analyze data that used to be shoe-horned into a repeated measures ANOVA design. Chapter 18 of Serious Stats introduces multilevel models by considering them as an extension of repeated measures ANOVA models that can cope with missing outcomes, time-varying covariates and can relax the sphericity assumption of conventional repeated measures ANOVA. They can also deal with other – less well known – problems such as having stimuli that are random factor (e.g., see this post on my Psychological Statistics blog). Last, but not least, multilevel generalised linear models allow you to have discrete and bounded outcomes (e.g., dichotomous, ordinal or count data) rather than be constrained by as assuming a continuous response with normal errors.
There are two main practical problems to bear in mind when switching to the multilevel approach. First, the additional complexity of the approach can be daunting at first – though it is possible to built up gently to more complex models. Recent improvements in availability of software and support (textbooks, papers and online resources) also help. The second is that as soon as a model departs markedly from a conventional repeated measures ANOVA, correct inferences (notably significance tests and interval estimates such as confidence intervals) can be difficult to obtain. If the usual ANOVA assumptions hold in a nested, balanced design then there is a known equivalence between the multilevel model inferences using t or F tests and the familiar ANOVA tests (and this case the expected output of the tests is the same). The main culprits are boundary effects (which effect inferences about variances and hence most tests of random effects) and working out the correct degrees of freedom (df) to use for your test statistic. Both these problems are discussed in Chapter 18 of the book. If you have very large samples an asymptotic approach (using Wald z or chi-square statistics) is probably just fine. However, the further you depart from conventional repeated measures ANOVA assumptions the harder it is to know how large a sample news to be before the asymptotics kick in. In other words, the more attractive the multilevel approach the less you can rely on the Wald tests (or indeed the Wald-style t or F tests).
The solution I advocate in Serious Stats is either to use parametric bootstrapping or Markov chain Monte Carlo (MCMC) approaches. Another approach is to use some form of correction to the df or test statistic such as the Welch-Satterthwaite correction. For multilevel models with factorial type designs the recommended correction is generally the Kenward-Roger approximation. This is implemented in SAS, but (until recently) not available in R. Judd, Westfall and Kenny (2012) describe how to use the Kenward-Roger approximation to get more accurate significance tests from a multilevel model using R. Their examples use the newly developed pbkrtest package (Halekoh & Højsgaard, 2012) – which also has functions for parametric bootstrapping.
My purpose here is to contrast the the MCMC and Kenward-Roger correction (ignoring the parametric bootstrap for the moment). To do that I’ll go through a worked example – looking to obtain a significance test and a 95% confidence interval (CI) for a single effect.
The pitch data example
The example I’ll use is for the pitch data from from Chapter 18 of the book. This experiment (from a collaboration with Tim Wells and Andrew Dunn) involves looking at the at pitch of male voices making attractiveness ratings with respect to female faces. The effect of interest (for this example) is whether average pitch goes up or done for higher ratings (and if so, by how much). A conventional ANOVA is problematic because this is a design with two fully crossed random factors – each participant (n = 30) sees each face (n = 32) and any conclusions ought to generalise both to other participants and (crucially) to other faces. Furthermore, there is a time-varying covariate – the baseline pitch of the numerical rating when no face is presented. The significance tests or CIs reported by most multilevel modelling packages with also be suspect. Running the analysis in the R package lme4 gives parameter estimates and t statistics for the fixed effects but no p values or CIs. The following R code loads the pitch data, checks the first few cases, loads lme4 and runs the model of interest. (You should install lme4 using the command install.packages(‘lme4’) if you haven’t done so already).
pitch.dat <- read.csv('http://www2.ntupsychology.net/seriousstats/pitch.csv')
head(pitch.dat)
library(lme4)
pitch.me <- lmer(pitch ~ base + attract + (1|Face) + (1|Participant), data=pitch.dat)
pitch.me
Note the lack of df and p values. This is deliberate policy by the lme4 authors; they are not keen on giving users output that has a good chance of being very wrong.
The Kenward-Roger approximation
This approximation involves adjusting both the F statistic and its df so that the p value comes out approximately correct (see references below for further information). It won’t hurt too much to think of it as turbocharged Welch-Satterthwaite correction. To get the corrected p value from this approach first install the pbkrtest package and then load it. The approximation is computed using the KRmodcomp() function. This takes the model of interest (with the focal effect) and a reduced model (one without the focal effect). The code below installs and loads everything, runs the reduced model and then uses KRmodcomp() to get the corrected p value. Note that it may take a while to run (it took about 30 seconds on my laptop).
The corrected p value is .0001024. The result could reported as a Kenward-Roger corrected test with F(1, 118.5) = 16.17, p = .0001024. In this case the Wald z test would have given a p value of around .0000435. Here the effect is sufficiently large that the difference in approaches doesn’t matter – but that won’t always be true.
The MCMC approach
The MCMC approach (discussed in Chapter 18) can be run in several ways – with the lme4 functions or those in MCMCglmm being fairly easy to implement. Here I’ll stick with lme4 (but for more complex models MCMCglmm is likely to be better).
First you need to obtain a large number of Monte Carlo simulations from the model of interest. I’ll use 25,000 here (but I often start with 1,000 and work up to a bigger sample). Again this may take a while (about 30 or 40 seconds on my laptop).
pitch.mcmc <- mcmcsamp(pitch.me, n = 25000)
For MCMC approaches it is useful to check the estimates from the simulations. Here I’ll take a quick look at the trace plot (though a density plot is also sensible – see chapter 18).
xyplot(pitch.mcmc)
This produces the following plot (or something close to it):
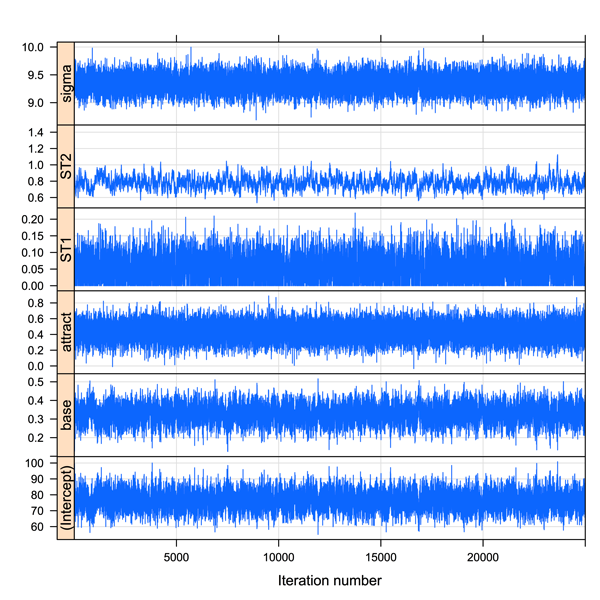
The trace for the fixed effect of attractiveness looks pretty healthy – the thich black central portion indicating that it doesn’t jump around too much. Now we can look at the 95% confidence interval (strictly a Bayesian highest posterior density or HPD interval – but for present purposes it approximates to a 95% CI).
HPDinterval(pitch.mcmc)
This gives the interval estimate [0.2227276, 0.6578456]. This excludes zero so it is statistically significant (and MCMCglmm would have given an us MCMC-derived estimate of the p value).
Comparison and reccomendation
Although the Kenward-Roger approach is well-regarded, for the moment I would reccomend the MCMC approach. The pbkrtest package is still under development and I could not always get the approximation or the parametric bootstrap to work (but the parametric bootstrap can also be obtained in other ways – see Chapter 18).
The MCMC approach is also preferable in that it should generalize safely to models where the performance of the Kenward-Roger approximation is unknown (or poor) such as for discrete or ordinal outcomes. It also provides interval estimates rather than just p values. The main downside is that you need to familiarize yourself with some basic MCMC diagnostics (e.g., trace and density plots at the very least) and be willing to re-run the simulations to check that the interval estimates are stable.
References
Judd, C. M., Westfall, J., & Kenny, D. A. (2012). Treating stimuli as a random factor in social psychology: A new and comprehensive solution to a pervasive but largely ignored problem. Journal of Personality and Social Psychology, 103, 54-69.
Halekoh, U., & Højsgaard, S. (2012) A Kenward-Roger approximation and parametric bootstrap methods for tests in linear mixed models – the R package pbkrtest. Submitted to Journal of Statistical Software.
Update
Ben Bolker pointed out that future versions of lme4 may well drop the MCMC functions (which are limited, at present, to fairly basic models). In the book I mainly used MCMCglmm – which is rather good at fitting fully crossed factorial models. Here is the R code for the pitch data. Using 50,000 simulations seems to give decent estimates of the attractiveness effect. Plotting the model object gives both MCMC trace plots and kernel density plots of the MCMC estimates (hit return in the console to see all the plots).
nsims <- 50000
pitch.mcmcglmm <- MCMCglmm(pitch ~ base + attract, random= ~ Participant + Face, nitt=nsims, data=pitch.dat)
summary(pitch.mcmcglmm)
plot(pitch.mcmcglmm)
Last but not least, any one interested in the topic should keep an eye on the draft r-sig-mixed-modelling FAQ for a summary of the challenges and latest available solutions for multilevel inference in R (and other packages).
R code formatted using Pretty R at inside-R.org

 POST
POST